Réduction de dimensionnalité : ACP et maintenant UMAP

L’Analyse en Composantes Principales (ACP) est une méthode statistique puissante et simple, utilisée pour réduire la dimensionnalité des données expérimentales tout en identifiant les relations entre les différentes variables. Développée il y a près d’un siècle, elle a trouvé des applications dans des domaines variés. Les biologistes l’utilisent pour analyser des données génomiques complexes ou pour modéliser les interactions entre espèces et facteurs environnementaux. Les physiciens s’en servent pour extraire des caractéristiques essentielles de spectres en spectroscopie ou pour détecter des signaux spécifiques dans des mesures multi-dimensionnelles, comme en astrophysique. Les économistes, quant à eux, s’appuient sur l’ACP pour repérer des tendances cachées dans des indices financiers ou des corrélations entre marchés. Sa polyvalence et sa simplicité en font un outil très largement utilisé par la communauté scientifique pour mieux comprendre des systèmes multidimensionnels.

Cependant, l’essor de l’intelligence artificielle et des data sciences a entraîné une explosion du volume et de la complexité des données à traiter. Dans ce contexte, les techniques traditionnelles comme l’ACP se heurtent à des limites lorsqu’il s’agit d'identifier des structures non linéaires ou des relations complexes dans des jeux de données à haute dimension.

Pour répondre à ces défis, des méthodes plus récentes, comme UMAP (Uniform Manifold Approximation and Projection), ont vu le jour. Développé en 2018 par Leland McInnes, John Healy, et James Melville, UMAP repose sur des fondements mathématiques modernes en théorie des graphes et en géométrie différentielle. Cette méthode permet de projeter des données de haute dimension dans des espaces à faible dimension tout en préservant, autant que possible, la structure globale et locale des données.

Fonctionnement de l’ACP

Application de l’ACP à un exemple bien connu

L'ACP est souvent utilisée comme une étape préliminaire dans les pipelines de traitement des données, en particulier lorsqu'il s'agit de travailler avec des modèles d'apprentissage automatique. Par exemple, dans le cadre d’un réseau de neurones, l’ACP peut être appliquée pour réduire la dimensionnalité des données d’entrée, ce qui permet d’utiliser de plus petits réseaux et de limiter le risque de surapprentissage.

Exemple sur le jeu de données « digits »

Le code ci-dessous utilise l’ACP pour réduire la dimensionnalité du jeu de données « digits » (fourni par la bibliothèque scikit-learn) et montre la même image avant et après la réduction :

UMAP pour « digits »

UMAP (Uniform Manifold Approximation and Projection) est une nouvelle technique de réduction de dimensionnalité, adapté à l'identification de liens entre les paramètres non linéaires, particulièrement efficace pour visualiser et découvrir de structures complexes dans des données de haute dimension. Ses principes de base sont :

1. Voisinage local
   UMAP construit un graphe de voisinage à partir de la distance (ou de la similarité) entre les points. Le nombre de voisins (n_neighbors) est un hyperparamètre pour contrôler la « résolution » à laquelle on observe la structure des données.

2. Fuzzy simplicial set
   Le graphe initial est transformé en une représentation floue (fuzzy) des données, conservant à la fois l’information locale et une partie de la structure globale.

3. Optimisation
   UMAP procède ensuite à une optimisation pour trouver une représentation en basse dimension qui préserve au mieux ces relations de voisinage. Les hyperparamètres (tels que n_neighbors, min_dist) influent sur la manière dont UMAP « déplie » la variété sous-jacente aux données.

Cette approche est souvent comparée à t-SNE, une autre technique de réduction non linéaire. UMAP présente l’avantage d’être plus rapide et de mieux préserver la structure globale, bien qu’il nécessite parfois plus de réglages pour parvenir à un résultat optimal, alors que l'ACP ne nécessite aucun hyperparamètre et donc aucun réglage.

Exemple de code UMAP sur « digits »

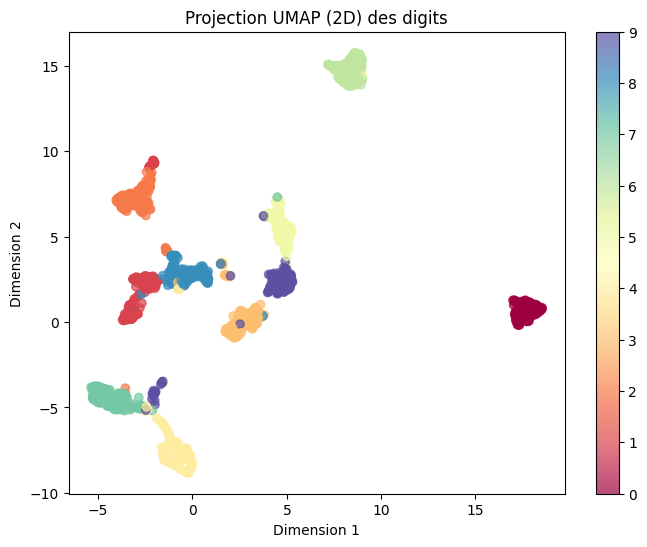
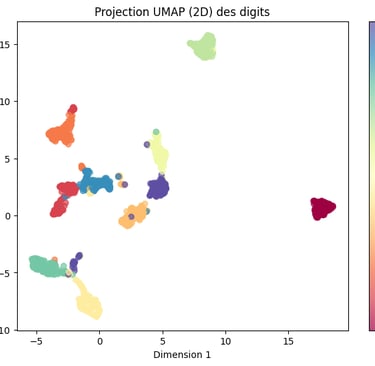
Au lieu de reconstruire l’image d’origine, on se contente de visualiser directement la projection en 2 dimensions ou 3 dimensions, où chaque point représente une image (un chiffre) et est coloré selon son label.

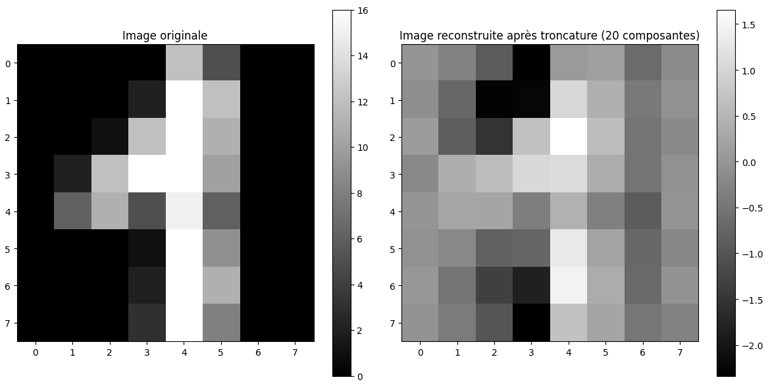
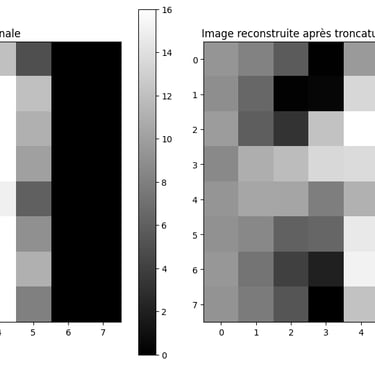
L'image ci-dessous est reconstruite après réduction de dimensionnalité avec l'Analyse en Composantes Principales (ACP), en conservant les 20 premières composantes principales. Bien que la structure globale de l'image soit plus ou moins préservée, certains détails fins sont perdus, illustrant l'effet de la troncature. L'image est en réalité représentée par un vecteur de 20 paramètres (les 20 premiers valeurs propres), utilisés pour la reconstruire comme une combinaison linéaire des 20 vecteurs propres associés à ces valeurs propres.
Dans un pipeline de traitement classique, on ne reviendrait pas à la base d'expression initiale : si, par exemple, je voulais réaliser une reconnaissance de caractères avec un réseau de neurones dense utilisé derrière l'ACP, je me contenterais d'utiliser directement ces 20 composantes principales comme entrée du modèle, réduisant ainsi la complexité du réseau et le risque de surapprentissage.

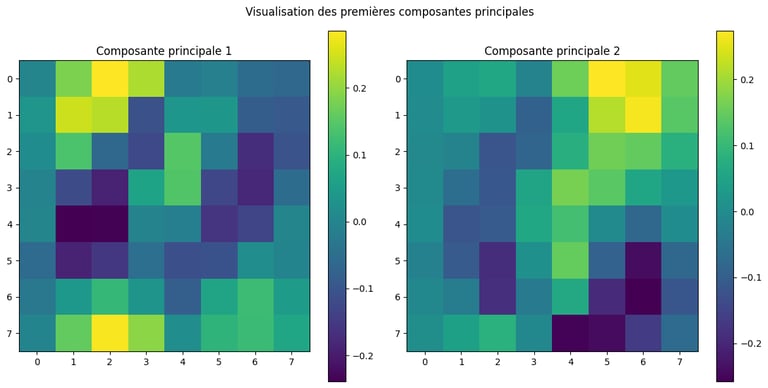
Voici, à titre d'illustration (ça n'est pas très parlant), les deux vecteurs propres représentés dans une matrice 8x8 :

Et voici l'évolution de la variance expliquée en fonction du nombre de composantes principales utilisées. On a choisi dans notre exemple de tronquer à 20 valeurs propres, ce qui correspond à environ 80 % de la variance expliquée :

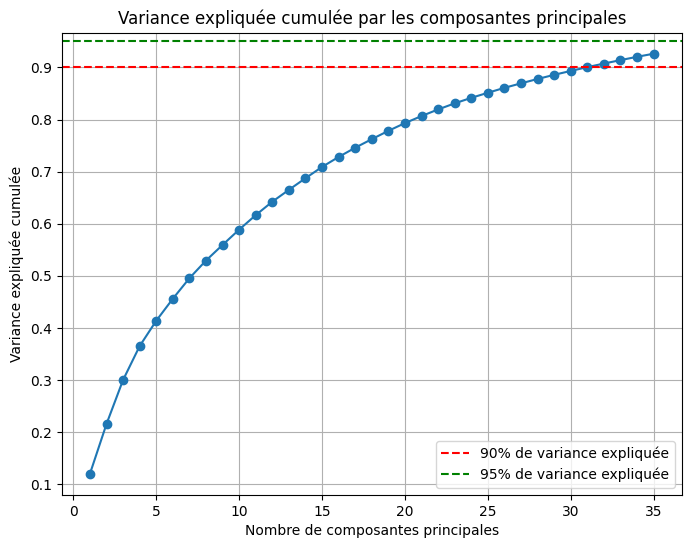
La projection en 3 dimensions donne l'image ci-dessous. Ce qui frappe à l'observation de ces graphiques, c'est qu'on pourrait presque se passer d'une étape de traitement supplémentaire tant la méthode UMAP est puissance : les données projetées en 2D ou 3D sont regroupées par chiffre de manière très explicite.

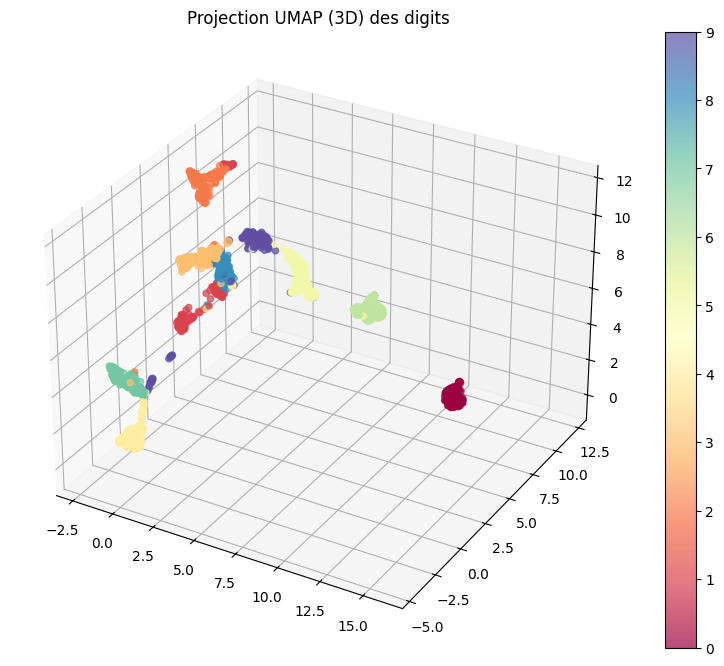
Conclusion

En conclusion, l’ACP et l’UMAP illustrent deux approches très différentes de la réduction de dimensionnalité. L’ACP, utilisée depuis près d’un siècle, reste un outil robuste grâce à sa simplicité mathématique et à sa rapidité, mais elle se limite aux relations linéaires entre les variables. À l’inverse, l’UMAP permet de capturer des structures complexes et non linéaires, ce qui en fait une méthode particulièrement adaptée à l’analyse d’images ou de signaux. Cette performance se paie toutefois par une plus grande complexité algorithmique et un coût de calcul plus élevé.

Il est d’ailleurs intéressant de noter que ces techniques, que l’on met aujourd’hui en œuvre en quelques lignes de code Python, étaient déjà développées dans les années 80. Un ami m’a raconté qu’à l’époque, il avait conçu ces outils (ACP, AMF) pour le laboratoire de biométrie d’Orsay (s’appuyant sur un processeur i80386 épaulé par un i387) ; le vrai luxe consistait alors à pouvoir visualiser, à la souris (et sur PC, c’était inédit), le nuage de points projeté dans l’espace engendré par les vecteurs propres les plus significatifs. Ses premiers jeux de données concernaient les qualités organoleptiques des vins, ainsi que leurs corrélations potentielles avec les cépages, l’ensoleillement, l’hygrométrie… bref, un vrai sujet d’intérêt (et de dégustation !)…

Aujourd’hui, l’UMAP s’avère particulièrement performant pour visualiser et explorer de grands jeux de données, offrant des regroupements explicites et clairs dès la réduction en deux ou trois dimensions. Pour l’exemple traité ici, cette efficacité rend l’étape de classification quasi superflue tant les clusters obtenus sont bien définis. Impressionnant…

Enfin, il est fascinant de constater à quel point ces méthodes, autrefois réservées à des configurations matérielles et logicielles très spécifiques, sont désormais accessibles en quelques lignes de code Python. Cela montre comment les outils modernes démocratisent l’analyse avancée de données, permettant des explorations rapides et intuitives, même pour des problématiques complexes.