Analyse modale avec des systèmes embarqués low cost

Dans cette partie, je vous propose de découvrir une expérience d’analyse modale menée sur une poutre modèle, à l’aide de systèmes embarqués conçus spécifiquement pour ce besoin. L’approche repose sur des capteurs accélérométriques MEMS low cost, associés à des microcontrôleurs ESP32 synchronisés par Wi-Fi. Une manipulation volontairement simple sur le plan mécanique (une poutre entre deux appuis en flexion), pour faciliter la comparaison entre expériences et modèle, mais qui révèle une belle richesse dans les données expérimentales, avec une mise en évidence nette des premiers modes propres de la structure.

Dans un article sur mon blog (https://selvasystems.net/la-synchronisation-de-plusieurs-systemes-embarques), j’expliquais comment nous avions mis au point un protocole de synchronisation « maison » entre plusieurs ESP32, capable de réduire l’écart d’horloge entre les boîtiers à un ordre de grandeur de 10 microsecondes (écart type). Cette synchronisation fine constitue le socle de notre démonstration : il est possible de faire de l’analyse modale sérieuse avec des systèmes embarqués low cost, synchronisés uniquement par radio — sans câblage, sans matériel onéreux.

Ce que je présente ici, ce sont les premiers résultats concluants d’une mesure vibratoire totalement sans fil, réalisée avec du matériel grand public qui, à l’origine, n’était pas du tout prévu pour ce type d’usage. Le principe est le suivant : plusieurs boîtiers d’acquisition, chacun équipé d’un accéléromètre MEMS, sont disposés en différents points de la poutre. Grâce à une synchronisation radio, les offsets entre les différents boitiers sont mesurés en continue. Un post-traitement permet ensuite de recaler et recombiner les données, révélant ainsi les caractéristiques vibratoires de la structure — et donc ses propriétés mécaniques fondamentales.

Pour illustrer simplement : imaginez que vous faites tinter une cloche. Si elle est fendue, elle ne sonnera pas de la même façon que si elle est intacte. La fréquence du son, mais aussi la manière dont la cloche vibre (les formes de vibration associées à chaque fréquence, qu’on appelle les modes propres), changent. C’est exactement cette « signature vibratoire » que nous cherchons à capter ici — et que ces petits boîtiers permettent d'enregistrer.

La problématique de la synchronisation

Ce n’est pas trivial, pour plusieurs raisons. D’abord, il faut pouvoir réactualiser régulièrement l’acquisition de l’offset de chaque boîtier, car à ces constantes de temps, la dérive des oscillateurs internes des microcontrôleurs devient significative. On parle d’une dérive typique de ±20 ppm, soit ±20 microsecondes par seconde. C’est suffisant pour dégrader sérieusement la cohérence des mesures si on ne corrige pas suffisamment régulièrement.

L’autre défi, c’est de réussir à maintenir cette synchronisation tout en continuant l’acquisition des signaux, sans que les deux tâches ne se gênent mutuellement dans le microcontrôleur. On cherche un équilibre fin entre précision temporelle et continuité d’enregistrement.

Et il faut être précis. Prenons un exemple simple : imaginez que vous souhaitez analyser le comportement vibratoire d’une structure, avec des capteurs accélérométriques échantillonnés à 1000 Hz (donc pour une structure vibrant à quelques centaines de Hz), en quatre points distincts. Pour capturer correctement les modes propres, il faut que les acquisitions soient rigoureusement synchronisées. À 1000 Hz, une période dure 1 milliseconde. Cela signifie qu’un décalage de quelques degrés en phase correspond à un décalage temporel de l’ordre de 10 microsecondes. Si vous dépassez ce seuil, le dépouillement modal perd en précision.

Ici la contrainte est un peu moins sévère. Nous étudions une poutre modèle dont les cinq premiers modes propres se situent en dessous de 50 Hz. Notre précision de synchronisation est donc largement suffisante pour notre application…

Concrètement, notre solution fonctionne avec un maitre, sorte de chef d’orchestre, et de plusieurs esclaves. Le maitre n’a pas pour fonction de travailler bien entendu : il n’opère aucune mesure. Il permet de déterminer l’offset et le drift pour chacun des esclaves.
On a recours à une approche statistique pour renforcer ces données. On utilise un filtre de Kalman.
Nos résultats montrent que le filtre converge très vite (de l’ordre de la vingtaine de seconde avec 4 boitiers esclaves) s’il est correctement initialisé.

Autre point : le temps d’acquisition de l’offset est largement plus court que le temps caractéristique de variation du drift. Ce qui est super. Bien entendu, plus on rajoute de boitiers à synchroniser, moins cela reste vrai. Notre système serait compatible avec la synchronisation fine d'au moins une trentaine de boitier avant de dégrader significativement la maitrise de l’offset (mais il y a plusieurs stratégies possibles pour améliorer cela).

La poutre modèle

Faute de mieux, les montants du dispositif ont été réalisés en PLA quasi plein. La poutre est pincée entre deux tubes en acier de 8 mm insérés dans la partie supérieure des montants, et l’ensemble est maintenu en place par de gros élastiques. Ce système ingénieux permet de bloquer efficacement la plupart des mobilités, à l’exception de la translation selon l’axe longitudinal de la poutre et de la rotation — on parle alors d’appuis glissants, bien connus en résistance des matériaux.

Les conditions d’appui ainsi que la disposition des boîtiers sont parfaitement symétriques. Cette symétrie facilite la modélisation théorique du comportement vibratoire de la poutre, et rend le traitement des données expérimentales plus lisible. D’ailleurs, une première analyse a été menée de manière analytique, et les résultats montrent déjà un bon accord entre le modèle et l’expérience.

Les fréquences propres de la poutre modèle ont été choisies de manière à rester comparables à celles observées sur un ouvrage réel. La fréquence fondamentale de notre montage est de 3,5 Hz, ce qui est très représentatif : un pont ou un ouvrage d’art présente généralement une fréquence fondamentale comprise entre 0,5 Hz et 4 Hz.

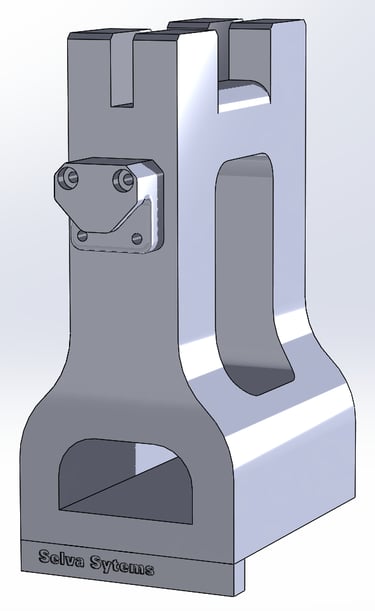
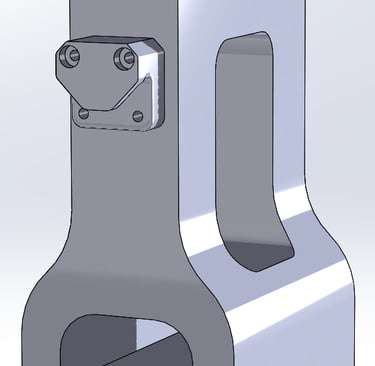
Pour l’excitation, je fais un lâchée avec une déformation imposée de 1 cm à la poutre. Je me mets à une position qui ne correspond pas à un ventre, pour aucun des premiers modes. Concrètement, j’impose la déformation au 7/24 de la poutre....

La poutre mesure 2.55m, 6mm de hauteur et 40 mm de large. Les appuis sont distants de 2m. Le système est symétrique. Les capteurs prennent placent à l/4, l/3, 2l/3 et 3l/4.

Le dépouillement des résultats expérimentaux

Synchronisation des mesures

Je fais une bonne part du post-traitement sur maltab/octave. Ce qui simplifie la vie coté embarqué.
Il y a plusieurs traitements préliminaires sur les signaux acquis pour chaque esclave afin de réduire la bande passante du capteur et de réduire le bruit.
Ensuite, on exploite les données issues du maitre pour « projeter » les données de tous les esclaves dans la base de temps du maitre par interpolation.

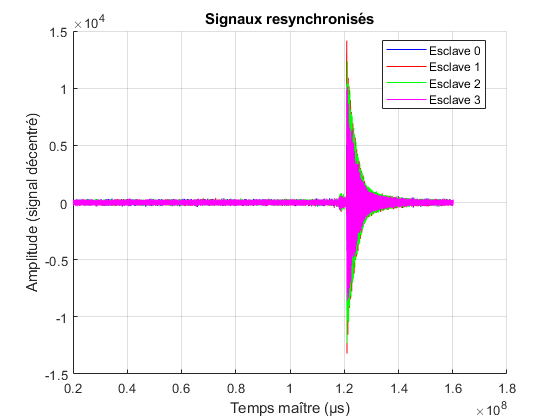
Pour illustrer ce processus (sur ces images les traitements du bruit n’est pas encore présents), le premier graphique représente les signaux temporels des 4 capteurs représentés à partir de leur temps machine respectif.

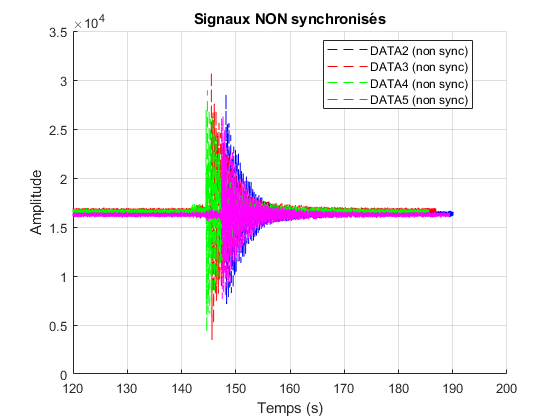
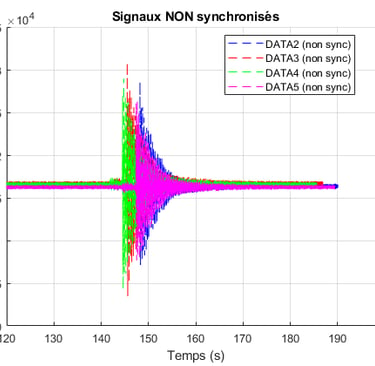
Comme en témoigne le second graphique, qui représente les mêmes signaux recentrés autour de leur moyenne et resynchronisés, notre méthode de synchronisation par radio marche très bien...

Répartition de puissance spectrale

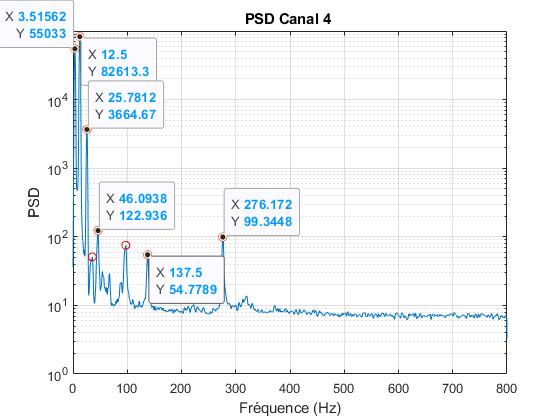
Une étape préliminaire avant de les injecter dans l’ADE pour l’analyse modale proprement dite est de déterminer les fréquences propres. Sous matlab/octave, j’ai calculé la densité spectrale de puissance (PSD) pour chacun des points de mesure. Le principe est simple : découpage en fenêtres temporelles, transformée de Fourier sur chaque segment, puis moyenne des spectres pour lisser le résultat. Ce traitement donne une première signature fréquentielle des modes, qui permet de valider la qualité des signaux avant toute exploitation plus poussée : il faut voir les fréquences propres de la poutre...

Et là, les mesures sont très exploitables comme visible sur le PSD suivant.

Comparaison avec calcul éléments finis

Et cerise sur le gâteau : ça colle très bien avec la petite simulation éléments finis réalisée. J’ai à peine eu besoin de retoucher les paramètres d’entrée dans mon modèle.
Dans le cas d’une poutre en deux appuis, symétrique, le comportement vibratoire est assez facile à prédire à la main — je le fais d’ailleurs avec mes étudiants.

Les fréquences propres suivent globalement la relation, avec n l'indice du mode et f0 la fréquence fondamentale :

Mais ici, le cas est un peu différent : on n’a plus affaire à une poutre de masse linéique constante.
En effet, chaque capteur — avec sa bride imprimée en PLA, sa platine support, le PCB et les composants — pèse environ 79 g. La poutre, elle, fait dans les 2 kg, et porte 4 capteurs. Ces masses ont une influence non négligeable sur les modes vibratoires. Il a donc fallu les modéliser dans l'étude éléments finis comme des masses ponctuelles.

En réalité, pour les modes les plus bas, leur influence reste limitée, et les résultats restent très proches de l’analytique. En revanche, pour les fréquences plus élevées, l’écart devient plus marqué, ce qui est tout à fait attendu.

Avec une densité de 7850 kg/m³, un coefficient de Poisson de 0,3 et un module d'Young de 210 GPa, une masse ponctuelle au droit des capteurs de 79g, les fréquences propres obtenues sont les suivantes : 3,33 Hz, 12,43 Hz, 25,52 Hz, 36,95 Hz et 49,05 Hz. L'accord avec les données expérimentales est très satisfaisant, avec un écart d’environ ±0.25 Hz jusqu'à 25 Hz et ±1 Hz au delà.

Les modes propres correspondants à chacune de ces fréquences sont présentés ci-dessous, et serviront de référence pour la comparaison avec les résultats expérimentaux fournis par l’ADE.

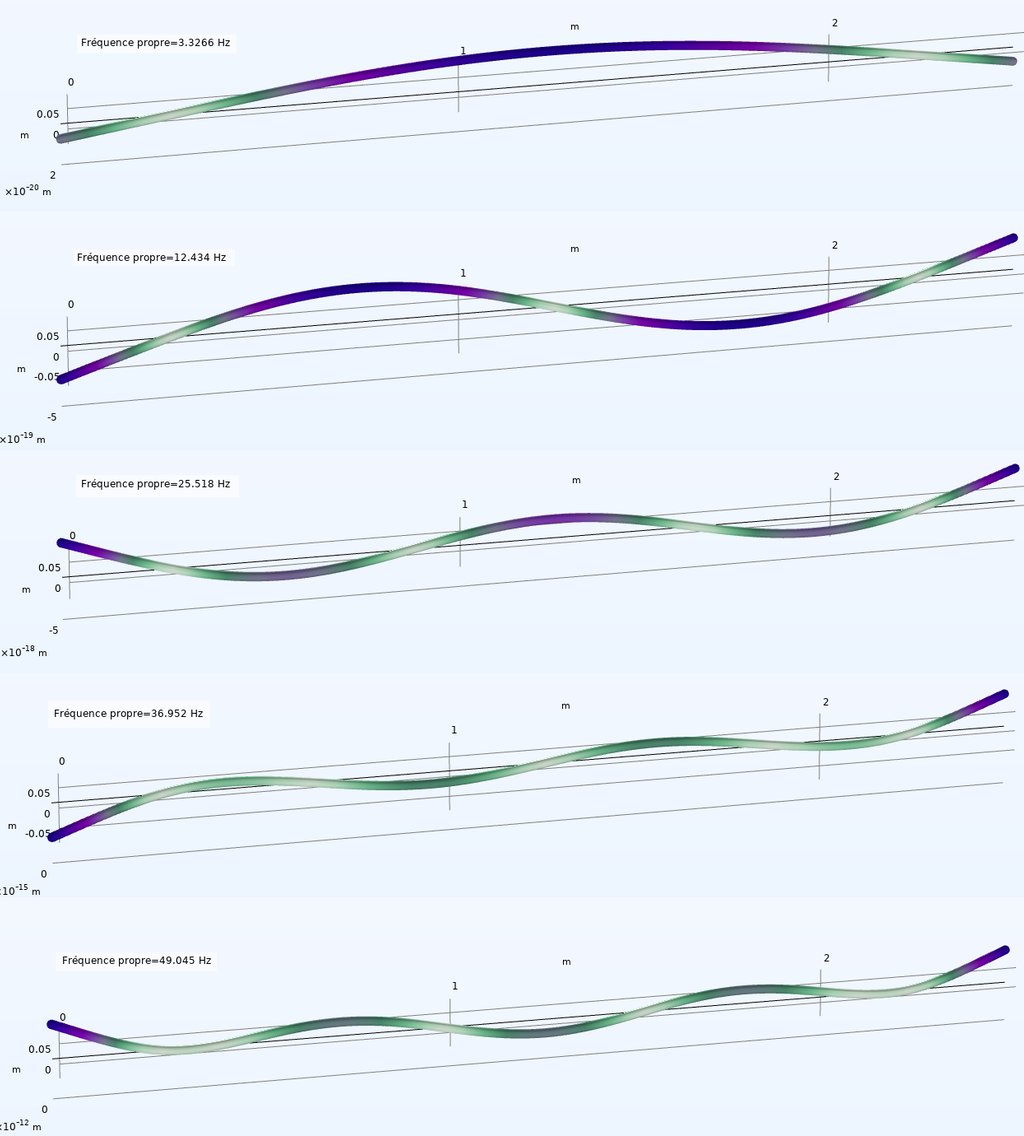
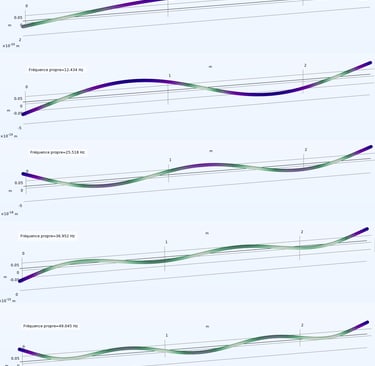
Méthode temporelle d'extraction des modes propres

Forcément, avec seulement quatre points de mesure fixes, ce n’est pas fou fou… On ne peut pas espérer une cartographie complète ni une animation précise de la déformée modale. Mais il n’en reste pas moins que les premiers modes apparaissent clairement. Et pour une manip aussi minimaliste dans ses moyens, c’est une belle réussite.

Voici donc les résultats pour les premiers modes, en lien avec les résultats et analyses présentés plus haut :

L’analyse modale a été réalisée à l’aide de l’ADE (Analyse de Décomposition en Espaces), une méthode d’identification temporelle. Le principe est de considérer les signaux comme la réponse libre (ou pseudo-libre) d’un système linéaire, et l’ADE extrait les modes propres (fréquences, amortissements, formes modales) à partir de la dynamique observée.

Techniquement, la méthode repose sur la construction d’une matrice de Hankel à partir des signaux, suivie d’une décomposition en sous-espaces. Elle est particulièrement adaptée à ce genre de manip ou au SHM (Structural Health Monitoring) en général, puisqu’elle fonctionne sans connaissance préalable du signal d’excitation. Elle permet d’identifier les modes dominants, même dans des conditions expérimentales peu contrôlées, ou lorsque la structure est soumise à son excitation naturelle. Par exemple, dans notre cas (on ne contrôle pas l'excitation). Ou dans le cas d’un pont, où les sources d’excitation peuvent être les rafales de vent, les voitures, les camions, les piétons marchant au pas militaire, etc…

J’ai prévu de consacrer un petit article à part entière au fonctionnement de cette méthode. Pour ma part je ne la connaissais pas avant d’avoir besoin de dépouiller ces résultats. Mais c’est une méthode simple et élégante — et surtout, très adapté aux essais où l'excitation n'est pas contrôlée.

Analyse des résultats modaux

Nous avons vu que l’analyse fréquentielle réalisée a permis d’identifier six modes propres, dont les cinq premiers sont situés entre 3,5 Hz et 52 Hz, et un sixième mode bien plus élevé à 274,6 Hz. Ces fréquences sont cohérentes avec le comportement attendu d’un système de type « poutre simplement appuyée », ou plus généralement d’un système linéaire vibrant dominé par la flexion.

Les fréquences mesurées suivent une progression approximativement quadratique, caractéristique des modes de flexion successifs. Des écarts vis-à-vis de la théorie idéale sont attendus, compte tenu des conditions aux limites réelles, des masses localisées, de l’amortissement et de la méthode d’excitation. Le saut de fréquence observé entre le cinquième et le sixième mode peut s’interpréter comme l’apparition d’un mode de torsion ou d’un mode local fortement raidi, dont la dynamique est très différente des premiers modes de flexion.

Les vecteurs modaux obtenus sont complexes, ce qui est habituel en analyse modale expérimentale. La partie imaginaire traduit à la fois la phase relative entre les canaux de mesure et l’effet de l’amortissement dans le système. Cette représentation complexe permet de capturer fidèlement l’information dynamique et de reconstruire la déformée complète de chaque mode.

D'ailleurs l’analyse de ces vecteurs modaux confirme la cohérence des résultats :

Le premier mode présente une déformée typique avec un maximum centré et un mouvement globalement en phase.
Le deuxième mode montre une symétrie centrale, comme attendu pour un mode pair avec un nœud au milieu de la poutre.
Le troisième mode, peu excité, reste faiblement visible dans les mesures, ce qui s’explique car l’excitation est placée à proximité d'un des nœuds à ce mode.
Le quatrième mode confirme de nouveau une symétrie centrale dans les amplitudes, en accord avec la nature du mode.

Une confirmation expérimentale particulièrement intéressante concerne la qualité de la synchronisation entre les voies de mesure. Dans les modes symétriques, on observe que les déphasages entre paires de capteurs placés de manière symétrique (notamment les canaux 0 et 3, ou 1 et 2 pour les modes 2 et 4) sont faibles. Cela témoigne d’une excellente synchronisation temporelle entre les voies. La faible dispersion de phase observée indique que le glissement résiduel associé à la résolution temporelle de notre synchronisation est faible. Ce résultat confirme la robustesse de l’acquisition multi-voies en mode embarqué, et constitue un point extrêmement positif du point de vue métrologique.

L’ensemble des résultats valide ainsi le très bon fonctionnement de la chaîne d’acquisition embarquée et la capacité à extraire des formes modales pertinentes avec des moyens low-cost radio-synchronisés. Pour être honnête, je ne m'attendais d'ailleurs pas à ce que cela fonctionne aussi bien et à rencontrer un accord entre expérience et modèle aussi satisfaisant : la comparaison entre les formes obtenues et les modes théoriques d’une poutre vibrante est une confirmation supplémentaire de la pertinence de l’approche.

Perspectives et manips complémentaires

Plusieurs pistes s’ouvrent pour affiner et prolonger cette preuve de concept. Parmi les axes immédiats de travail :

Répéter les essais, afin de renforcer la validité des résultats par superposition et analyse statistique. Cette étape est cruciale pour confirmer la reproductibilité des signatures vibratoires extraites.
Fabriquer une nacelle de test (cf. photo ci-dessous), à suspendre à la tige d’un pot vibrant. Elle permettra de soumettre deux boîtiers à une accélération identique pendant plusieurs heures. L’objectif : observer l’évolution de l’écart de phase entre les signaux acquis, en fonction de la fréquence d’excitation.
Ce test, réalisé aussi avec un seul boîtier, permettra de caractériser le bruit de mesure, en comparant différentes configurations matérielles : types de MEMS, traitements du signal, réglages de la chaîne d'acquisition.
Modifier les conditions aux limites de la poutre (appuis), pour étudier les effets sur les fréquences propres et la distribution spectrale. Par exemple, un appui central ouvrirait la voie à d’autres formes de réponse vibratoire, potentiellement plus complexes.

Et ensuite ?

Pour passer du prototype au déploiement sur le terrain, d’autres étapes sont à franchir :

Concevoir un boîtier étanche, robuste, et en produire une vingtaine pour les fixer sur un véritable pont — l’objectif final.
Tester la robustesse de la synchronisation non plus sur quelques heures comme ici, mais sur plusieurs jours, en conditions extérieures (variations thermiques, humidité, pertes de connexion…).
Ajouter une couche réseau dans le firmware embarqué, capable de gérer les interruptions de signal, les déconnexions temporaires, et d’assurer une communication résiliente entre les nœuds — même en cas de défaillance d’un boîtier.